傅里叶叠层计算成像

傅里叶叠层显微成像是一种能够同时实现大视场和高分辨率图像的计算成像技术。传统的傅里叶叠层算法通过迭代算法综合不同频域低分辨率图像的信息获得高分辨大视场的物体图像，算法的复原效果与低分辨图像的数据量相关，复原图像质量与采集时间和计算成本需要进行平衡。为了能够减少数据采集量，加强复原算法的鲁棒性，提高图像的复原质量实现超分辨，本研究提基于先验神经网络的先验特性构建新的傅里叶叠层显微成像方法。

傅里叶叠层计算成像 Fourier Ptychographic Imaging

• “Sha J, Qiu W, He G, et al. Improving the resolution of Fourier ptychographic imaging using an a priori neural network[J]. Optics Letters, 2023, 48(23): 6316-6319.”
• “陈奕灿, 吴霞, 罗志, 等. 基于深度学习的傅里叶叠层显微成像[J]. Laser & Optoelectronics Progress, 2020, 57(22): 221106.”
• “https://arxiv.org/abs/2003.07460”

基于网络先验的傅里叶叠层成像

双网络单通道结构

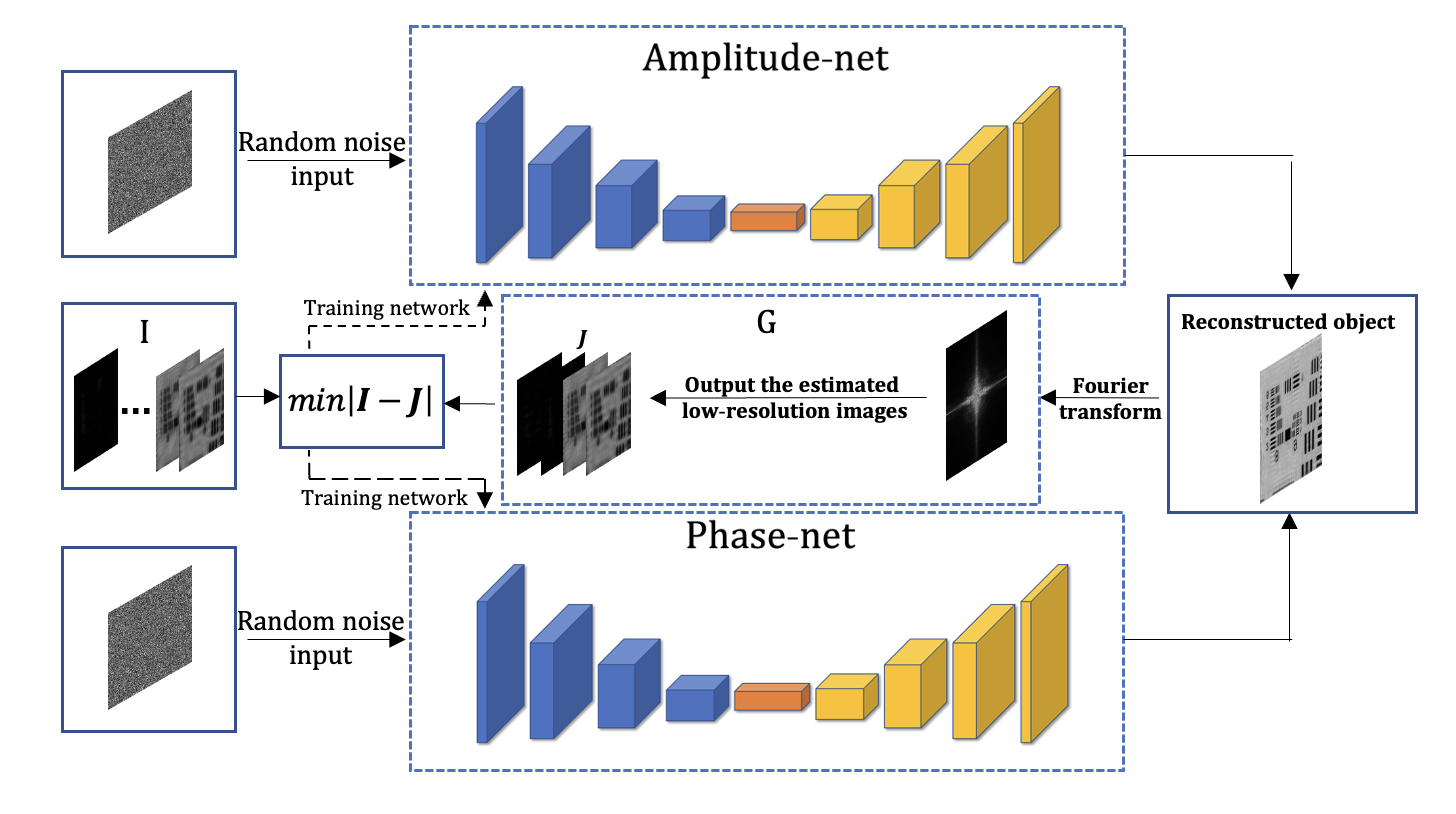
双网络单通道结构

单 LED 光照条件下双网络单通道结构仿真与实验

双网络单通道结构仿真结果

左侧是幅度，右侧是相位。(a)是原始图像，(b)是用GS算法复原的结果，(c)是用MFP复原的结果，(d)是用我们提出的方法复原的结果。

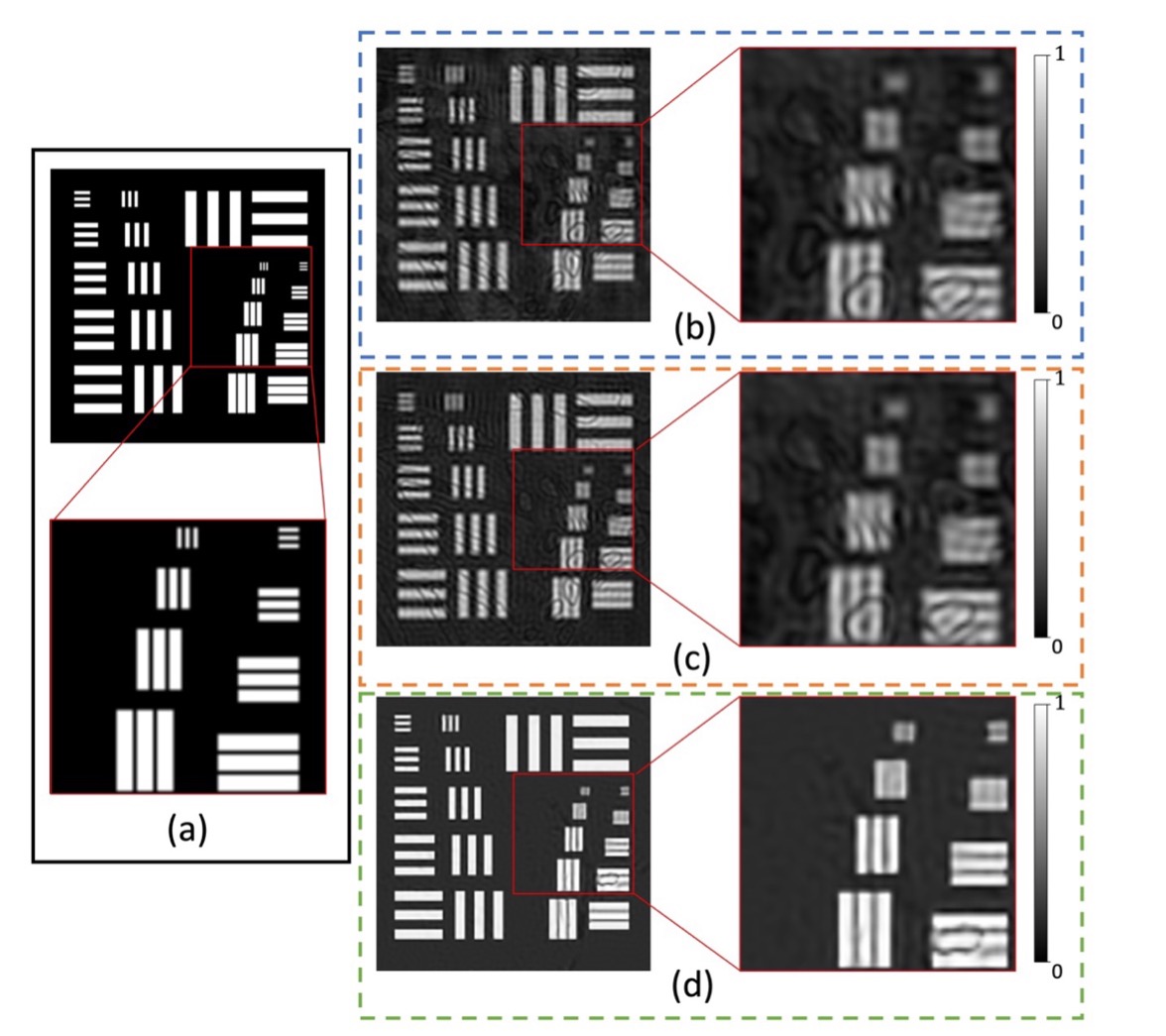
双网络单通道结构复原USAF实验结果

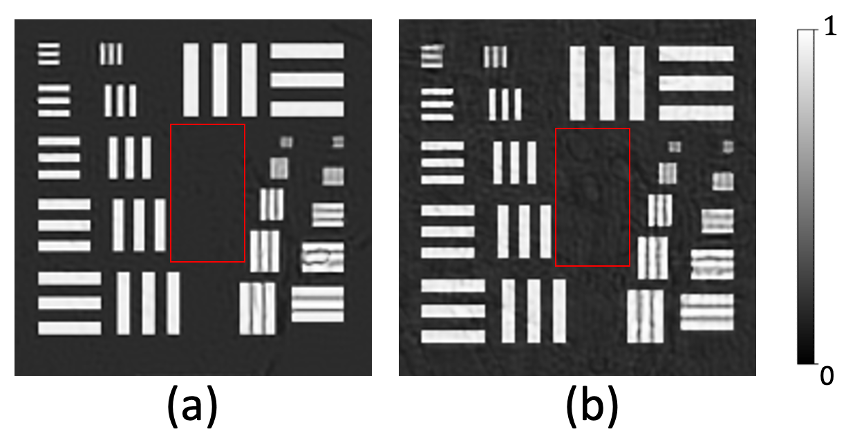
(a)是采集得到的低分辨率原始图像，(b)和(c)是我们算法在69和97盏中心区域LED的条件下复原的高分辨率图像。

GS算法分别在69，97，109，137盏中心LED灯的条件下复原的结果，对应图中(a)-(d)

MFP算法分别在69，97，109，137盏中心LED灯的条件下复原的结果, 对应图中(a)-(d)

双网络单通道结构复原细胞实验结果

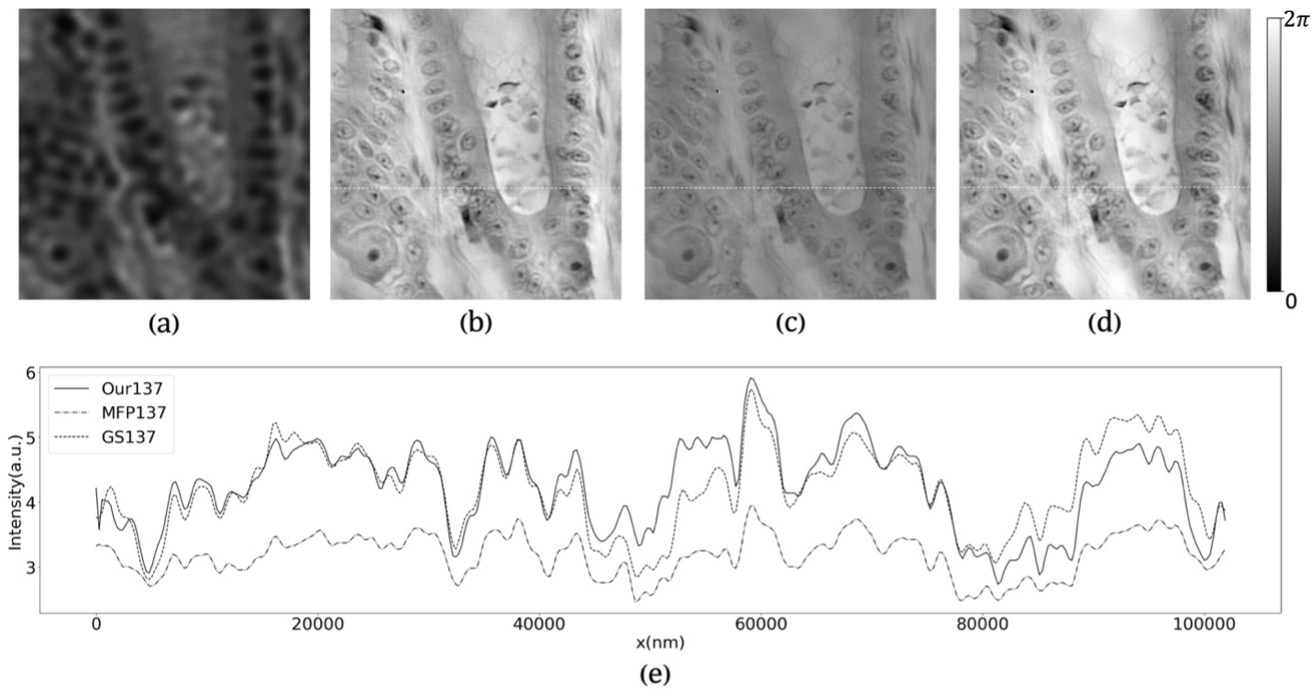
225张数据下相位复原图。(a)是采集得到的亮场原始低分辨率图像，(b)是GS算法复原的相位结果。(c)是MFP复原的相位结果。(d)是我们算法的复原结果。(e)是我们的方法与GS算法和MFP算法相比，整个图像的相位值分布线。

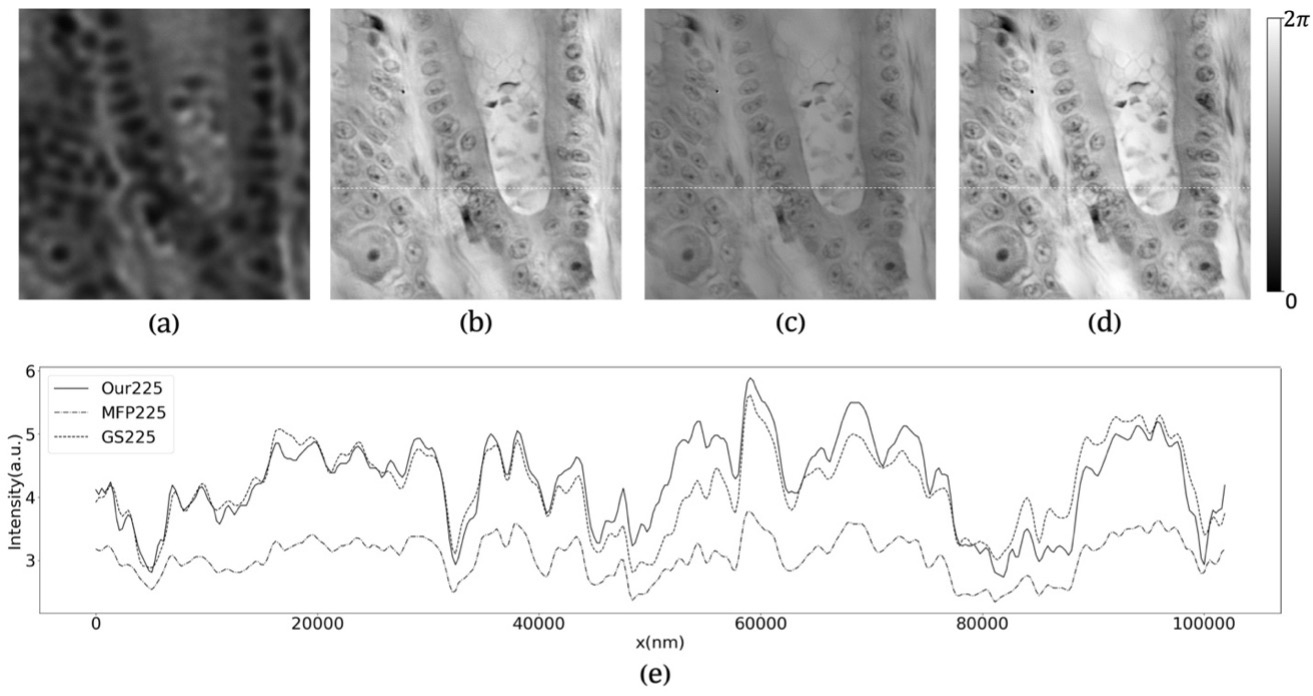
137张数据下相位复原图。(a)是采集得到的亮场原始低分辨率图像，(b)是GS算法复原的相位结果。(c)是MFP复原的相位结果。(d)是我们算法的复原结果。(e)是我们的方法与GS算法和MFP算法相比，整个图像的相位值分布线。

双网络单通道结构抗噪声实验结果

噪声对比实验结果，(a)是GS算法的复原结果，(b)是自适应步长算法的复原结果，(c)是我们的复原结果。

单网络双通道结构

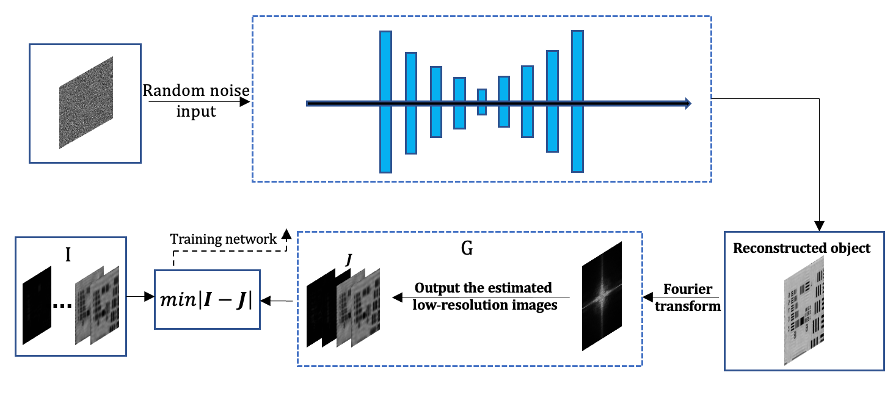
单网络双通道结构

单 LED 光照条件下单网络双通道结构仿真研究

单网络双通道结构对比双网络单通道结构仿真结果

左侧是幅度，右侧是相位。(a)是双子网络结构的复原图，(b)是单网络双通道结构的复原图。

基于先验神经网络的多灯复用傅里叶叠层成像方法

多灯复用下先验神经网络结构

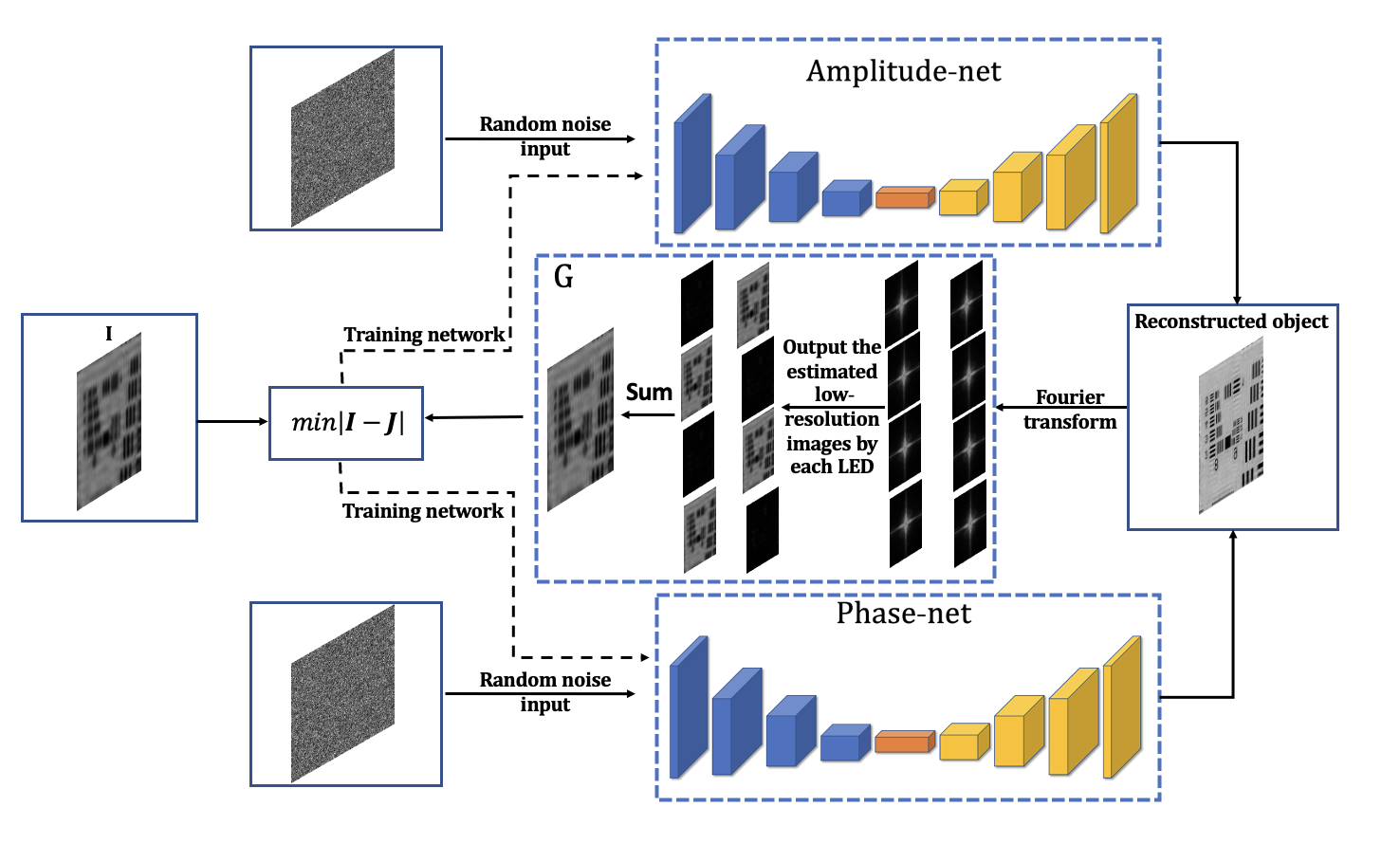
多灯复用网络图

基于合成数据的多 LED 灯复用研究

有冗余信息下的多灯复用仿真实验

有信息冗余下的复原结果。(a)和(c)是在模拟8盏LED复用合成293张数据量下分别用传统方法和我们方法的复原结果，(b)是在模拟4盏LED复用合成586张数据量下传统方法的复原结果。

无冗余信息下的多灯复用仿真实验

无冗余下的复原结果。(a)和(c)是在模拟8盏LED复用合成37张数据量下分别用传统方法和我们方法的复原结果，(b)是在模拟4盏LED复用合成74张数据量下传统方法的复原结果。

不同 LED 复用数量仿真实验

不同LED数量照射下复原结果。(a)-(d)是在模拟2盏、4盏、8盏、16盏下，分别合成得到152张、76张、37张、19张数据下我们方法的复原结果。

16 盏 LED 复用下的仿真实验

16盏LED复合下不同数据量仿真结果。(a)-(c)是用我们方法复原模拟16盏LED复用合成37张、50张、129张数据的复原结果，(d)是传统方法模拟16盏LED复用合成129张数据下复原结果。

8LED 灯复用实验复原研究

有冗余信息下的多灯复用实验

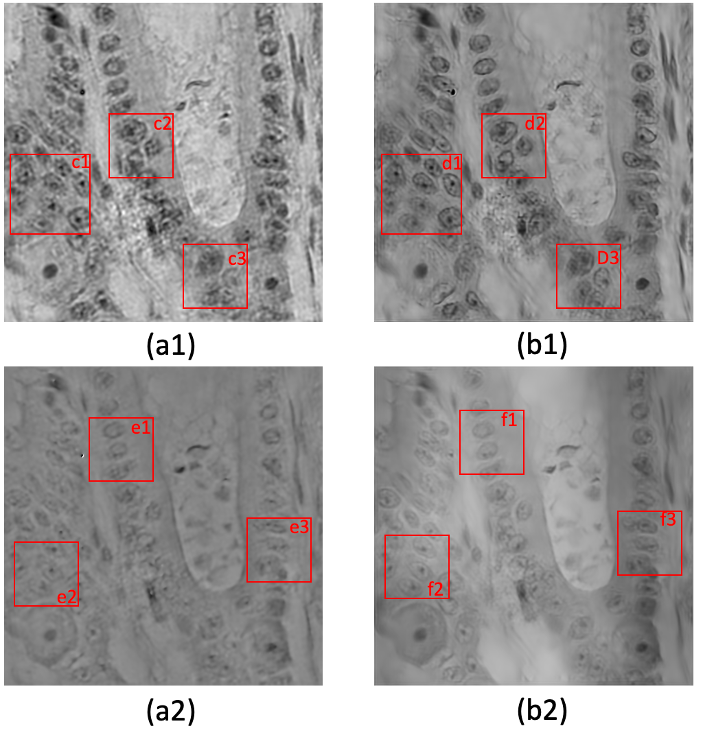
8盏LED复用293张数据下不同方法实验结果。上面是复原的幅度信息，下面是复原的相位信息。(a1)和(a2)是传统算法EMFP的复原结果，(b1)和(b2)是我们的复原结果。

无冗余信息下的多灯复用实验

8盏LED复用得到37张数据下不同方法实验结果。上面是复原的幅度信息，下面是复原的相位信息。(a1)和(a2)是传统算法EMFP的复原结果，(b1)和(b2)是我们的复原结果。